Rectas (Paralelas y Perpendiculares)

Rectas paralelas

Son dos rectas que no tienen ningún punto en común, o son coincidentes. Dos rectas, contenidas en un plano, son paralelas si o bien son una y la misma recta (son rectas coincidentes) o, por el contrario, no comparten ningún punto. De manera semejante, en el espacio, dos planos son paralelos si bien son uno y el mismo plano o bien no comparten ningún punto.

Definiciones de Rectas Paralelas

Axioma de unicidad

El axioma que distingue a la Geometría euclídea de otras geometrías es el siguiente: En un plano, por un Punto exterior a una Recta pasa una y sólo una paralela a dicha recta.

• Rectas paralelas son aquellas rectas que se encuentran en un mismo plano, presentan la misma pendiente y que no presentan ningún punto en común, esto significa que no se cruzan, ni tocan y ni siquiera se van a cruzar sus prolongaciones. Uno de los ejemplos más populares es el de las vías de un tren.
  • Dos rectas son paralelas si sus vectores directores son paralelos, es decir, si éstos son linealmente dependientes.
  • Dos rectas son paralelas si tienen sus vectores directores iguales.
  • Dos rectas son paralelas si tienen sus pendientes iguales.
  • Dos rectas son paralelas si los coeficientes de x e y respectivos son proporcionales.
  • Dos rectas son paralelas si forman un ángulo de 0º.

Propiedades de las Rectas Paralelas

Las propiedades que ostentan las mismas son:

• Reflexiva (toda recta es paralela a si misma)
• Simétrica (si una recta es paralela a otra, aquella será paralela a la primera)
• Transitiva (si una recta es paralela a otra y esta a su vez es paralela a una tercera, la primera será paralela a la tercera recta),
  • corolario de la propiedad transitiva (dos rectas paralelas a una tercera serán paralelas entre sí) y (todas las rectas paralelas presentan la misma dirección)

En tanto, los teoremas vinculados a las rectas paralelas nos dicen: que en un plano, dos rectas perpendiculares a una tercera serán paralelas entre sí; por un punto exterior a una recta, pasará siempre una paralela a esa recta; y si una recta corta a una de dos paralelas, cortará también a la otra, siempre hablando en un plano. El trazado de las líneas paralelas puede llevarse a cabo con regla y escuadra o con regla y compás.

Ángulos determinados por dos rectas paralelas cortadas por una transversal

Dos rectas cualesquiera cortadas por una tercera determinan ocho ángulos.

Ángulos entre paralelas

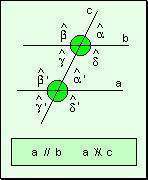
Clasificación

De acuerdo a la ubicación de los mismos se clasifican en:

• Ángulos interiores: Están ubicados en la zona comprendida entre las rectas paralelas .
• Ángulos exteriores: Los ángulos que no son interiores se denominan ángulos exteriores.
• Ángulos correspondientes: Si dos ángulos están ubicados de un mismo lado de la transversal, uno es interior y el otro es exterior, se les llama ángulos correspondientes.

• Los ángulos correspondientes entre paralelas son iguales.
• Recíprocamente, si dos rectas cortadas por una tercera forman ángulos correspondientes iguales, las rectas son paralelas.

• Ángulos alternos:

• Ángulos alternos internos: Si dos ángulos están situados en distintos semiplanos con respecto a la transversal y ambos son internos, se les llama ángulos alternos internos.
• Los ángulos alternos internos entre paralelas son iguales. Recíprocamente, si dos rectas cortadas por una tercera forman ángulos alternos internos iguales, las rectas son paralelas.
• Ángulos alternos externos: Si dos ángulos están situados en distintos semiplanos con respecto a la transversal y ambos son externos, se les llama ángulos alternos externos.
• Los ángulos alternos internos entre paralelas son iguales. Recíprocamente, si dos rectas cortadas por una tercera forman ángulos alternos externos iguales, las rectas son paralelas.

• Ángulos conjugados

• Ángulos conjugados internos: Si dos ángulos están situados en un mismo semiplano con respecto a la transversal y ambos son internos, se les llama ángulos conjugados internos.

Los ángulos conjugados internos entre paralelas son suplementarios. Recíprocamente, si dos rectas cortadas por una tercera forman ángulos conjugados internos suplementarios, las rectas son paralelas.

• Ángulos conjugados externos: Si dos ángulos están situados en un mismo semiplano con respecto a la transversal y ambos son externos, se les llama ángulos conjugados externos.

Rectas Perpendiculares 

Dos rectas en el plano son perpendiculares si entre ellas forman un Ángulo recto (en rigor, se formen cuatro ángulos rectos). En un sistema de coordenadas, el producto de las pendientes de ambas rectas es -1

 Rectas Perpendiculares

• Dos rectas son perpendiculares cuando al cortarse forman cuatro Ángulos iguales de 90º.
• Dos rectas son perpendiculares si sus vectores directores son perpendiculares.
• Dado un Punto perteneciente a una recta o exterior a ella, por él pasa una y sólo una perpendicular a dicha Recta.

Dos rectas son perpendiculares si sus Vectores directores son perpendiculares es decir el producto de los vectores es igual a cero

Si dos rectas son perpendiculares tienen sus pendientes inversas y cambiadas de signo.

La relación de perpendicularidad se puede dar entre:

• Rectas: dos rectas coplanarias son perpendiculares cuando, al cortarse, dividen al plano en cuatro regiones iguales, cada una de los cuales es un ángulo recto. Al punto de intersección de dos rectas perpendiculares se le llama pie de cada una de ellas en la otra.
• Semirrectas: dos semirrectas son perpendiculares, cuando conforman ángulos rectos teniendo o no el mismo punto de origen.
• Planos: dos planos son perpendiculares cuando conforman cuatro ángulos diedros de 90º.
• Semiplanos: dos semiplanos son perpendiculares cuando conforman ángulos diedros de 90°; generalmente, compartiendo la misma recta de origen.

Además, puede existir una relación de perpendicularidad entre los cuatro elementos anteriores, tomados de dos en dos.

Si dos rectas al cortarse forman Ángulos adyacentes congruentes, son perpendiculares. Por analogía, si dos planos al cortarse forman ángulos diedros adyacentes congruentes, son perpendiculares. Los lados de un ángulo diedro y sus semiplanos opuestos determinan dos planos perpendiculares).

DEFINICIÓN.- Un triángulo Rectángulo es un Triángulo uno de cuyos ángulos es recto. El lado opuesto al ángulo recto se llama hipotenusa y los otros dos lados son los catetos.

DEFINICIÓN.- Una recta y un plano son perpendiculares, si se intersecan y además, toda recta en el plano que pase por el punto de intersección es perpendicular a la recta dada.

Propiedades de las Rectas Perpendiculares

Las propiedades que ostentan las mismas son:

• Reflexiva: La perpendicularidad no cumple con el carácter reflexivo.
• Simétrica: Si una recta es perpendicular a otra, ésta es perpendicular a la primera.
• Transitiva: La perpendicularidad no cumple con el carácter transitivo.

Teoremas

• Teorema: En un plano, dos rectas perpendiculares a una tercera son paralelas.
• Teorema: En un plano dado y por un punto dado de una recta dada, pasa una y solamente una recta perpendicular a la recta dada.
• Teorema de la mediatriz: En un plano dado, la mediatriz de un segmento es la recta perpendicular al segmento en su punto medio.
• Teorema: Desde un punto externo dado, hay a lo menos una recta perpendicular a la recta dada.

COLORARIO: Ningún Triángulo tiene dos Ángulos rectos.

• Teorema - Si B y C equidistan de P y Q entonces todo punto entre B y C también equidistan de P y Q.

COROLARIO: Se da un segmento AB (con raya arriba) y la recta L en el mismo plano. Si dos puntos de L equidistan de A y B, entonces la mediatriz de AB (con raya arriba).

• Teorema - Si una recta es perpendicular a dos rectas que se intersecan en su Punto de intersección, entonces es perpendicular al plano que contiene a las rectas.

Características de los triángulos(según su lado)

Tipos de triángulos según los lados.

Basándonos en la medida relativa de los lados de un triángulo podemos hacer la siguiente clasificación de triángulos según los lados:

• Equiláteros: son triángulos que tienen todos sus lados iguales.
• Isósceles: son triángulos que tienen dos de sus lados iguales.
• Escalenos: son triángulos que tienen todos sus lados desiguales.
  

Tipos de triángulos según sus ángulos.

Según la amplitud de sus ángulos, podemos clasificar los triángulos de la siguiente manera:

• Rectángulos: son triángulos que tienen un ángulo recto (90º). El lado opuesto al ángulo recto se denomina hipotenusa y los otros dos son los catetos. La hipotenusa siempre es mayor que cualquiera de sus catetos. En un triángulo rectángulo los dos ángulos agudos son complementarios, suman 90º.
• Acutángulos: son triángulos que tienen los tres ángulos agudos (miden menos de 90º).
• Obtusángulos: son triángulos que tienen un ángulo obtuso (mayor de 90º)

Rectas y puntos notables de un triángulo.

Mediatrices y circuncentro de un triángulo.

Las mediatrices de un triángulo son las propias mediatrices de los lados que lo conforman, las perpendiculares al lado por el punto medio. Las mediatrices de un triángulo se cortan en un punto conocido como circuncentro. Este punto es el centro de la circunferencia circunscrita la triángulo. Es decir, la circunferencia en la cual queda inscrito el triángulo.

Para hallar el circuncentro y trazar la circunferencia circunscrita basta con trazar dos de las mediatrices de un triángulo. El punto en el que se corten será el circuncentro. Hacemos centro en él y abriremos el compás hasta cualquiera de los vértices del triángulo. Trazamos la circunferencia, que deberá pasar por los vértices restantes.

Video donde se explica

Bisectrices e incentro de un triángulo.

Las bisectrices de un triángulo serán las propias bisectrices de los ángulos internos del triángulo. Estas se cortaran en un único punto conocido como incentro. Este será el centro de la circunferencia inscrita al triángulo. Es decir, la circunferencia que se encuentra dentro del triángulo y es tangente a sus tres lados.

Para hallar el incentro y trazar la circunferencia inscrita bastará con trazar dos de las bisectrices de un triángulo. El punto en el que se corten será el incentro. Desde él trazaremos una perpendicular a cualquiera de los lados. El segmento que va desde el incentro al punto de corte de la perpendicular con el lado es el radio de la circunferencia inscrita. Con centro en el incentro y el radio mencionado trazamos la circunferencia inscrita, que deberá ser tangente a los tres lados del triángulo.

Video donde se explica

Alturas y ortocentro de un triángulo.

Las alturas de un triángulo son las rectas que pasando por un vértice son perpendiculares al lado opuesto o a la recta prolongación de este. El punto de corte de la altura con el lado se conoce como pie de la altura. El punto de corte de las alturas de un triángulo es el ortocentro.

Al unir los pies de las alturas obtenemos el triángulo órtico. Este triángulo tiene como propiedad que sus lados son el camino más corto para ir desde un lado del triángulo original a los otros dos.

Video donde se explica 

Medianas y baricentro de un triángulo.

Las medianas son los segmentos que unen los vértices con los puntos medios de los lados opuestos. El punto de corte de las medianas de un triángulo se llama baricentro, también conocido como centroide. Este punto es el centro de gravedad del del triángulo, ya que cada una de las medianas divide al triángulo en otros dos que tienen el mismo área. Otra propiedad interesante del baricentro es que siempre se encuentra a un tercio de la mediana respecto al lado y dos tercios respecto al vértice.

Video donde se explica

Tipos De Angulos

Angulo Adyacentes

son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas a veces pueden tener hasta 4 lados, dependiendo de los vértices. De allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un ángulo llano (180°), sin poseer ningún punto interior en común.

Angulo Obtuso

El ángulo obtuso es el espacio entre dos rectas que comparten un mismo vértice cuya inclinación o abertura es mayor que 90 grados (90°) y menor que 180 grados (180°).

y se los pueden encontrar, por ejemplo, en los triángulos obtusángulos ya que se caracterizan precisamente por tener uno de sus ángulos obtuso, o sea, mayor a 90 grados y menor a 180 grado.

Angulo Recto

Un ángulo recto es aquel que mide 90 (sexagesimales). Su amplitud medida en otras unidades es: π/2 radianes y 100^g (centesimales). Sus dos lados son dos semirrectas perpendiculares, y el vértice es el origen de dichas semirrectas.

Euclides lo define de este modo: Cuando una línea recta que está sobre otra hace que los ángulos adyacentes sean iguales, cada uno de los ángulos es recto, y la recta que está sobre la otra se llama  perpendicular a la otra recta.

Angulo Agudo

El ángulo agudo es el espacio entre dos rectas que comparten un mismo vértice cuya inclinación o apertura es mayor que 0 grados (0°) y menor que 90 grados (90°).

Angulo Complementario y Suplementario

Complementario

Los ángulos complementarios son aquellos ángulos cuyas medidas suman ${\displaystyle 90^{\circ }}$ grados sexagesimales, es decir, que si dos ángulos complementarios son a su vez consecutivos, los lados no comunes de estos forman un ángulo recto.

Suplementario

Dos ángulos ${\displaystyle \alpha }$ y ${\displaystyle \beta }$ son ángulos suplementarios, si suman ${\displaystyle 180^{\circ }}$ (grados sexagesimales).

• Un ángulo es o tiene suplementario si es menor que ${\displaystyle 180^{\circ }}$.

• El valor de ${\displaystyle 180^{\circ }}$ es el mismo que dos ángulos rectos, ${\displaystyle \pi }$ rad o ${\displaystyle 200^{g}}$ grados centesimales.